Por qué 6 es un número perfecto, pero 7 definitivamente no lo es

No todo el mundo puede serlo, pero 6 es un número perfecto.
Sabemos por 2.300 años, que es considerablemente más largo que la gran mayoría de los otros 50 miembros conocidos del exclusivo club.
¿Por qué es perfecto?
Porque 6 = 1 + 2 + 3
Los números perfectos son iguales a la suma de sus divisores: 6 se puede dividir entre 1, 2 y 3, y cuando suma estos números, el resultado es 6.
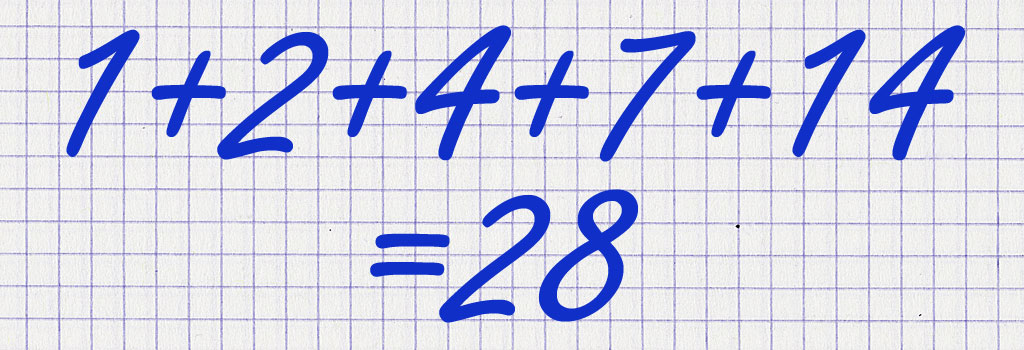
La historia de los números perfectos es parte de una de las ramas más antiguas y fascinantes de las matemáticas: la teoría de números.
El primero en referirse a ellos no fue otro que Euclides, en su influyente obra «Los elementos», publicada en año 300 AC.
Había descubierto cuatro números perfectos y en su libro reveló una forma segura de encontrar a otros. Seguro, pero difícil y lento.
Lea también: El planeta Pi tarda 3,14 días en orbitar y se parece a la Tierra
Si tiene curiosidad por saber cuál era la fórmula, aquí va. De lo contrario, omita lo que está entre las líneas verdes.

Esto es, paso a paso, lo que dijo:
«Si una multitud de números se define continuamente en doble proporción …»
Es decir, por ejemplo, 1, 2, 4, 8, 16, 32, 64…
«… (comenzando) de una unidad, hasta que cualquier suma agregada se convierta en un primo.. «
Entonces, agreguemos un número primo (divisible solo por 1 y él mismo)
1 + 2 + 4 + 8 + 16 = 31
«… y la suma multiplicada por el último (número) da un (número), entonces el (número como este) creado será perfecto«
Por lo tanto, la suma se multiplica por el último número de la secuencia: 31 veces16 = 496… y el resultado debe ser un número perfecto.
¿ESTÁ?
496 se puede dividir por 1, 2, 4, 8, 16, 31, 62, 124 y 248. Si lo sumamos, el resultado es 496, por lo que en realidad es un número perfecto.

Euclid no dejó solo cuatro de esos números seleccionados:6, 28, 496 y 8128– pero inspiró a las generaciones posteriores de matemáticos a continuar la búsqueda.
La búsqueda larga. Pasarían más de 1750 años antes de que se identificara otro número perfecto.
Lea también: Estudiante de la UNAM, el mejor mexicano en concursos de matemáticas
Antes de eso, otro matemático griego, el Neopitaghoric Nicomachus de Gerasa (c.60-c.120 DC) les dio un carácter más místico.
Adivinar
En su «Introducción a la aritmética», Nicomachus hizo una clasificación de números que incluía los perfectos y colocó los demás en su lugar.

Los perfectos ya habían sido definidos por Euclides, pero si la suma de los divisores de este más, eran abundante; si di menos, discapacitado.
Pero no se limitó a nombrarlos: los números pueden haber sido creados iguales, pero para Nicomachus algunos eran más iguales que otros.
Cuando hay mucho, dijo «hay exceso, superfluo, exageración y abuso; en el caso de muy poco, hay deseos, faltas, privaciones e insuficiencias«
El contraste con estar en pie de igualdad era marcado.
«Sucede virtud, única medida, decoro, belleza y cosas así, de las cuales lo más ejemplar es ese tipo de número llamado perfecto«
Tu calificación ha dejado su huella. Los números perfectos se han vuelto, al menos por un tiempo, divinos.
Miles de cálculos después …
En 1456, alguien registró otro número perfecto en un manuscrito medieval: 33550336.
Y en 1588, el matemático italiano Pietro Antonio Cataldi encontró otros dos: 8589869056 Y 137438691328.
¡Puedes imaginar cuánto trabajo les debe haber costado hacer esto sin una computadora!
Es impresionante … y el octavo número perfecto que se descubriría dos siglos después, incluso más.

Fue identificado nada menos que por el gran Leonhard Euler en 1772, tenía 19 dígitos y, según el matemático inglés del siglo XIX Peter Barlow, era «probablemente el más grande por descubrir«.
Yo estaba equivocado.
Dos décadas después de su muerte, se encontró el noveno año, gracias a los avances en tecnología y teoría de números. Los períodos de tiempo entre un descubrimiento y otro se han acortado hasta el punto de que en este milenio se han encontrado casi uno al año.
Lea también: Las grandes cuestiones que aún quedan por descubrir en matemáticas
Ahora conocemos un total de 51 números perfectos. El más reciente tiene 49,724,095 dígitos.
El extraño indescriptible
Si los vieras a todos, notarías que, sin excepción, son iguales.
Esto dio lugar a uno de los misterios más antiguos de las matemáticas: la conjetura de los números perfectos impares.
Una conjetura es una regla que nunca ha sido probada, en este caso sería algo así como «todos los números perfectos son pares».
Esto es algo que no podremos decir hasta que se resuelva la gran pregunta que se hicieron los matemáticos desde René Descartes en el siglo XVII hasta el mineral noruego Øystein en el siglo XX: ¿Hay números impares perfectos?

Varias mentes brillantes se movieron en busca de la respuesta.
Sin embargo, lo único que sabemos hasta ahora es que si hay debe ser superior a 10³⁰⁰, ya que la conjetura fue verificada computacionalmente hasta ese valor sin encontrar ninguno.
Pero al final del día …
¿Para qué valen la pena?
Dado el tamaño y la cantidad de luminarias en el mundo matemático que dedicaron tiempo y materia gris a números perfectos, puede ser natural imaginar lo importante que es.
Y nada más agradable que encontrar una respuesta magnífica, como la que dio David E. Joyce, profesor de Matemáticas e Informática de la Universidad de Clark, en el portal Quora.
“Los criterios tradicionales de importancia en la teoría de números son estéticos e históricos. Lo que la gente piensa que es importante es lo que les interesa. Esto difiere de una persona a otra ”, dice.
En pocas palabras, son importantes porque son interesantes… que mejor razon! Y si ha leído hasta aquí, probablemente esté de acuerdo.
Además, una de las cosas más fascinantes de las matemáticas es que suele revelar maravillas que solo con el tiempo llegamos a comprender.
Recuerda que puedes recibir notificaciones de BBC World. Descarga la nueva versión de nuestra aplicación y actívalas para no perderte nuestro mejor contenido.
