En el infinito, las rectas y los cuadrados tienen el mismo número de puntos.

En posts anteriores establecimos que dos conjuntos tienen el mismo tamaño si existe una correspondencia biunívoca entre los elementos de ambos conjuntos. La aplicación de este principio a la teoría del infinito de Cantor nos lleva a la extraña pero válida conclusión de que el número de puntos en un segmento de línea es el mismo que el número de puntos en un cuadrado. Para mostrar que esto es cierto, aquí hay una imagen de un segmento de línea de longitud unitaria y un cuadrado unitario.
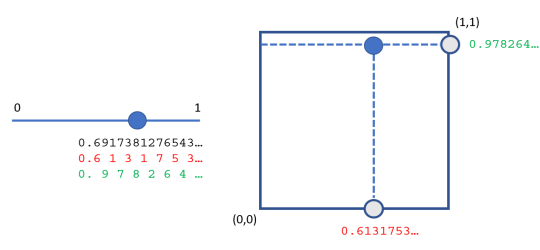
Elijamos un punto en el segmento de recta. Di 0.6917381276543… . Se muestra con un gran punto azul en el segmento de línea izquierdo. Si este punto corresponde a un numero irracional, continúa para siempre sin repetirse o mostrar un patrón perceptible.
Vamos a dividir este número en dos números. El primer número es cualquier otro dígito. Debajo del segmento de línea se muestra en rojo este número, es decir, 0,6131753…. Los dígitos restantes forman el segundo número, que se muestra en verde. Es 0.978264… .
Un solo número entre cero y uno se puede dividir en dos números entre cero y uno. Podemos tomar estos dos números y como las coordenadas x e y en el cuadrado unitario que se muestra a la derecha. Definen el punto azul que se muestra en el cuadrado de la derecha. Por lo tanto, el punto azul del segmento de línea se asigna al punto azul del cuadrado.
Para cada punto en el segmento de línea, hay uno y solo un punto azul en el cuadrado. El tamaño de los conjuntos infinitos en un segmento de línea y en un cuadrado es exactamente el mismo. Una extensión de este argumento muestra que el número de puntos en un cubo es el mismo que el número de puntos en un segmento de línea. Esto es contrario a la intuición y extraño.
También es posible el mapeo inverso de cuadrado a segmento de línea. Toma las dos coordenadas que definen el punto azul en el cuadrado y mézclalas para obtener un número. Dos números entre cero y uno siempre se pueden combinar para formar un solo número entre uno y cero. Este nuevo número es el punto en el segmento de línea.
Dado que hay un mapeo uno a uno de cada punto en el segmento de línea a cada punto en el cuadrado, el número de puntos en un segmento de línea es el mismo que el número de puntos en un cuadrado.
¿Pero no puedes dibujar un segmento de línea y un cuadrado en una hoja de papel y hacer el mapeo? ¿No es esto una ilustración del infinito en la realidad? No. Se supone que cada punto se mide con una precisión infinita. La precisión en la realidad es siempre finita. Por lo tanto, la conclusión de que no hay infinitos en la realidad sigue siendo fuerte.
Este resultado contrario a la intuición, impulsado por la teoría de los infinitos de Cantor, es extraño. Sin embargo, es una propiedad válida del infinito.
Próximo: Mostraremos que toda la Biblioteca del Congreso está codificada digitalmente en casi todos los números elegidos al azar.
Aquí está la Parte 1: Por qué Infinity no existe en la realidad. Unos pocos ejemplos mostrarán los resultados absurdos que se derivan de la suposición de que el infinito existe en el mundo que nos rodea, así como en las matemáticas. En una serie de cinco publicaciones, explico la diferencia entre lo que significa, y lo que no significa, infinito como concepto.
y
Parte 2. El infinito ilustra que el universo tiene un comienzo. Las consecuencias lógicas de un pasado literalmente infinito son absurdas, como lo demostrará una simple ilustración. Los absurdos que crearía un tiempo pasado infinito, si bien no son una prueba matemática definitiva, son evidencia sólida de que nuestro universo tuvo un comienzo.
También es posible que desee leer: Si tu puedes manipular el infinito en matemáticas. Los hiperreales son más grandes (y más pequeños) que su número promedio, ¡y mejores! (Jonathan Barlett)





